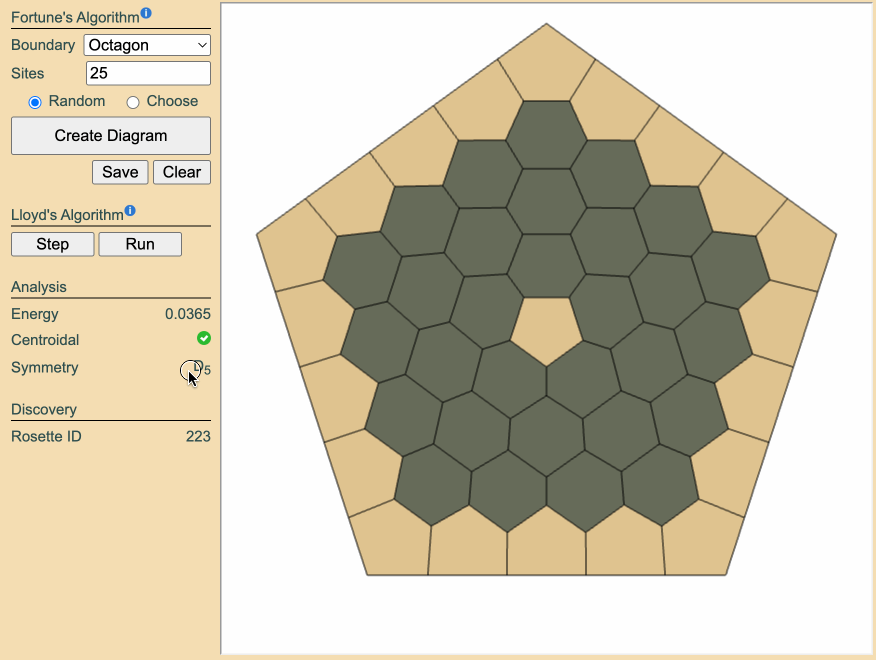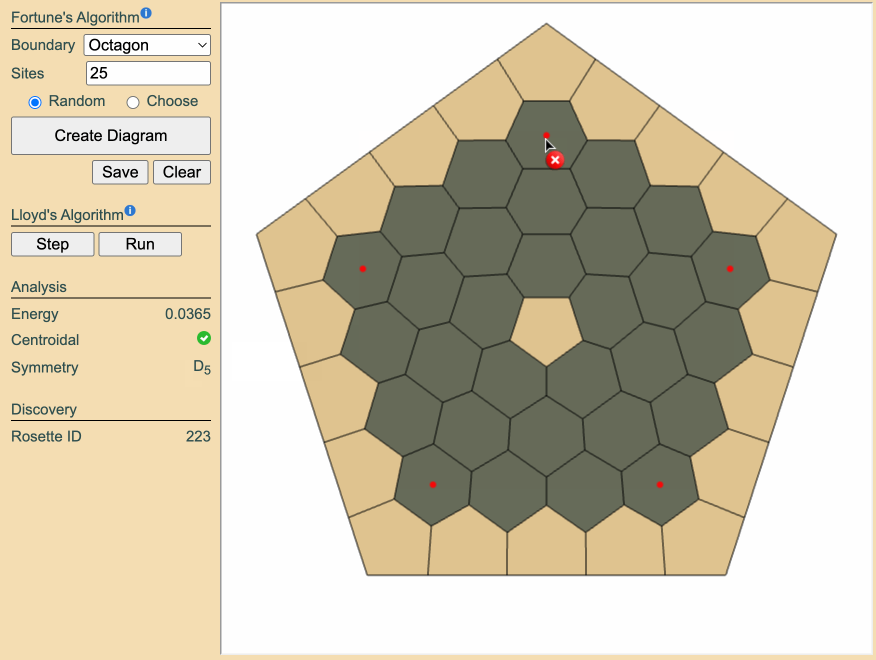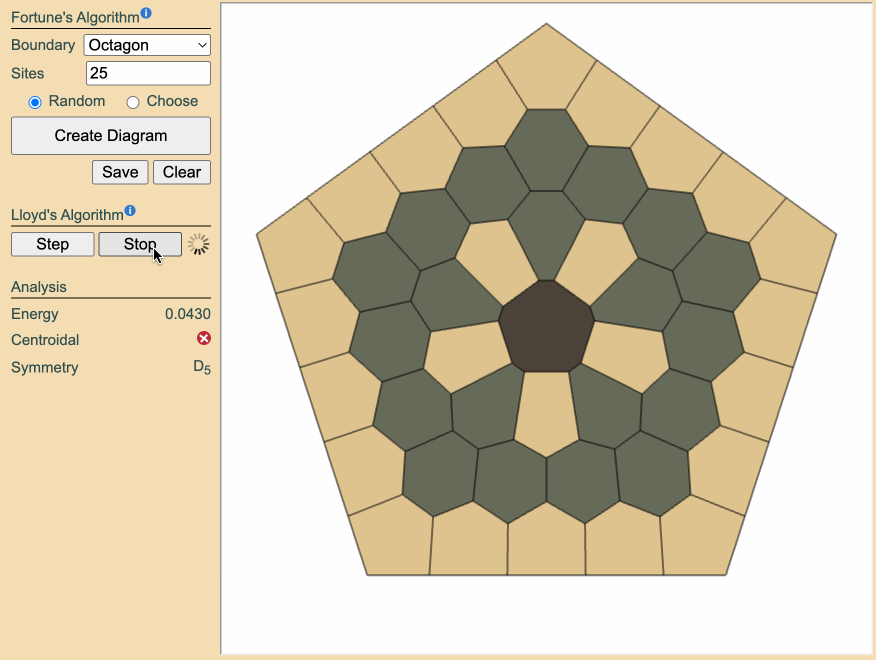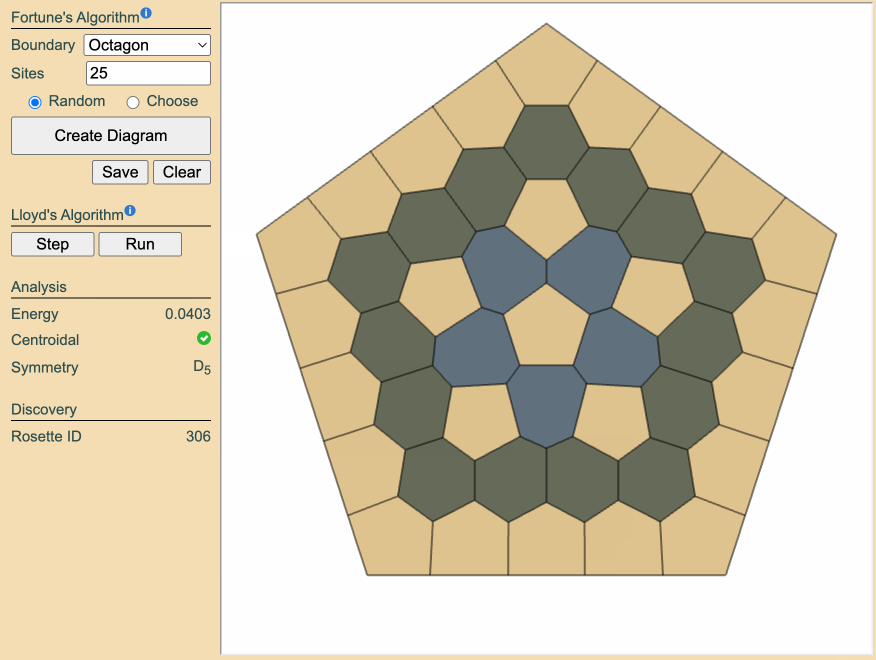
Create Diagram to generate an initial Voronoi diagram. After
that, click Run to apply Lloyd's relaxation, transforming your diagram into a
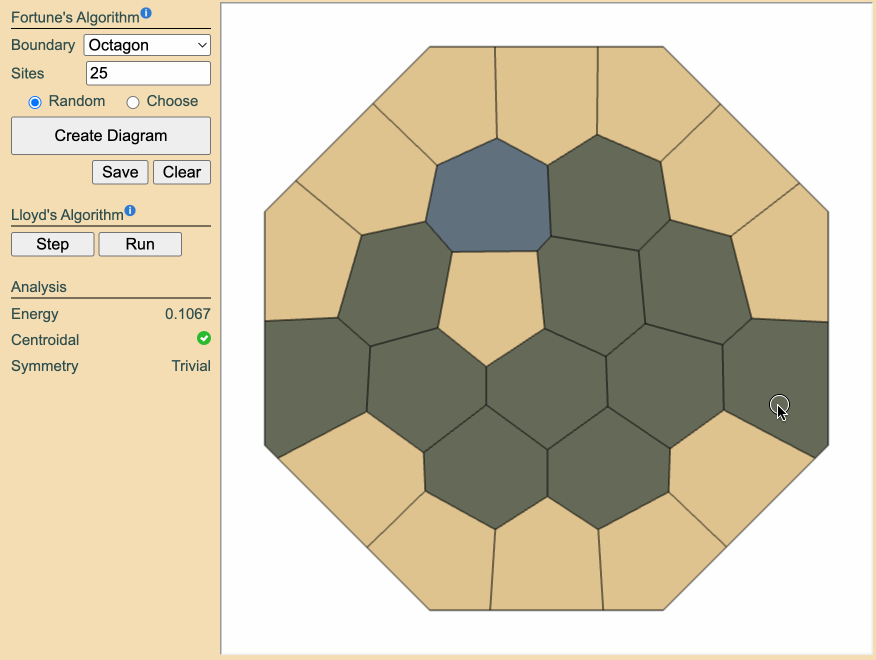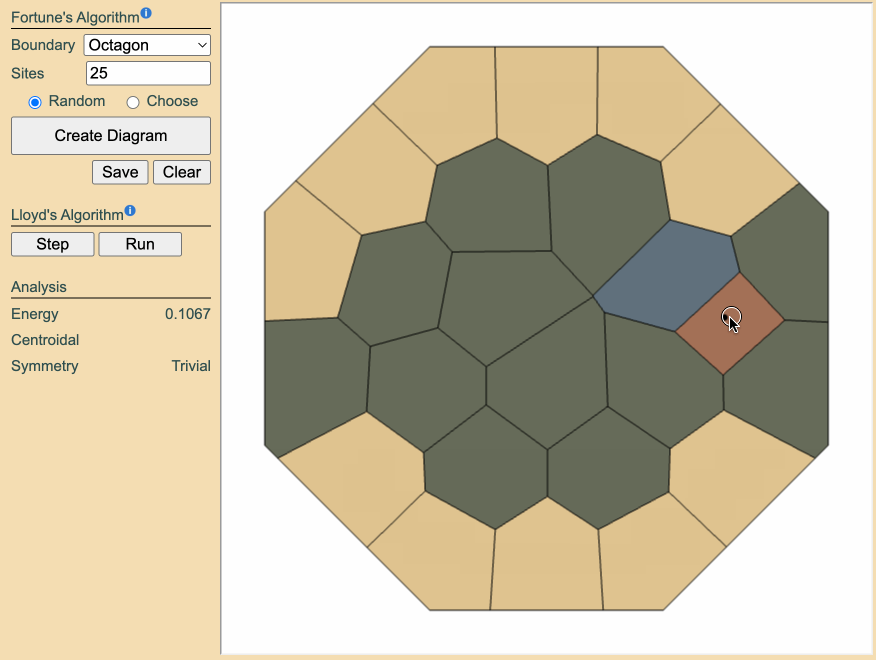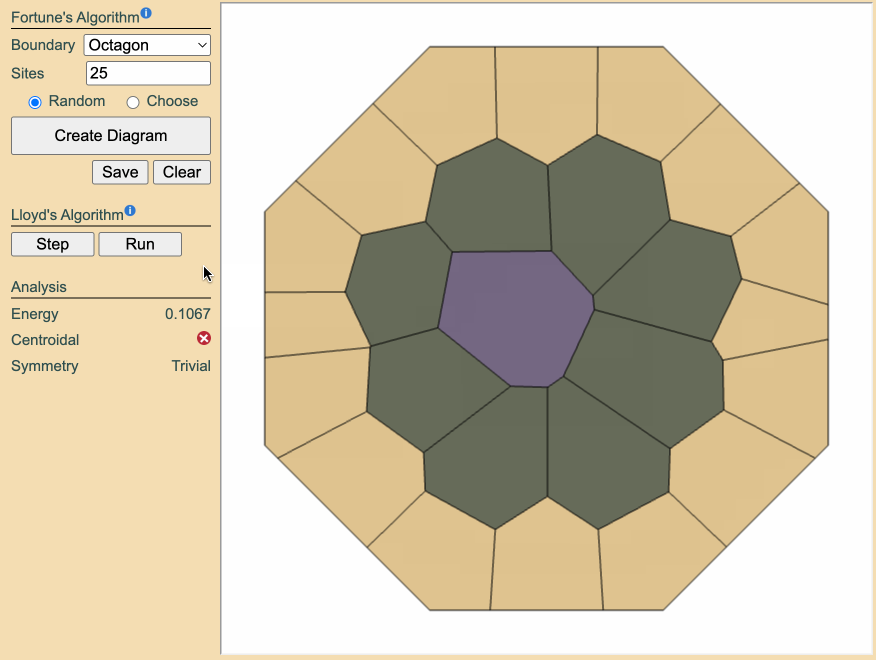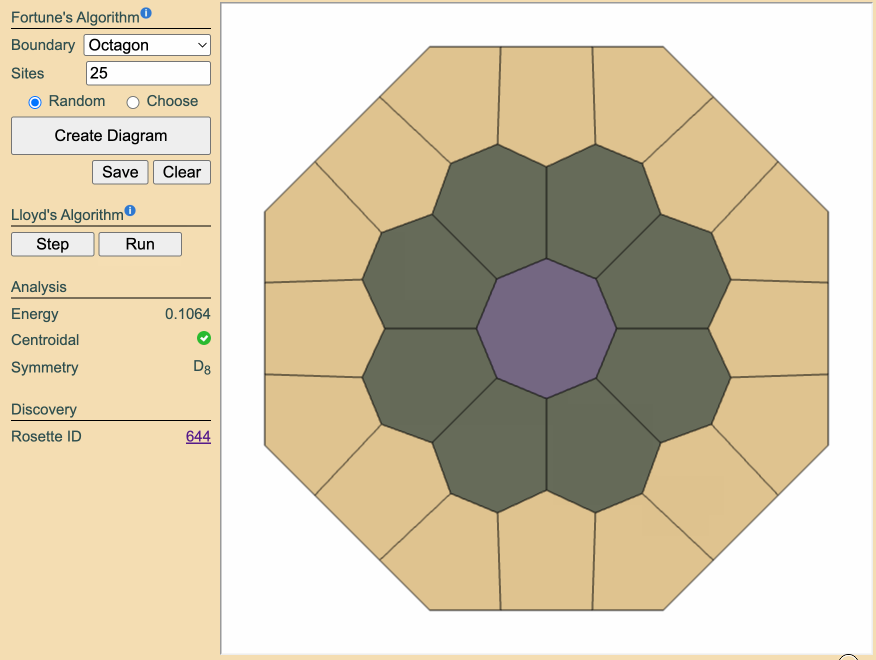
centroidal Voronoi diagram-a Rosette.
Do you want to find new Rosettes but aren't sure how to get started? Or perhaps you've discovered a few already, but want a more targeted approach. This guide dives deeper into the formation of Rosettes, exploring how their mathematical properties can help you uncover new and interesting patterns, more intentionally and efficiently. It builds directly upon the concepts introduced in the Rosette Theory pages. Take a moment to read those now if you haven't already.
The easiest way to start creating Rosettes is directly in the Rosette Studio. Select a boundary type, choose the number
of sites, and click Create Diagram to generate an initial Voronoi diagram. After
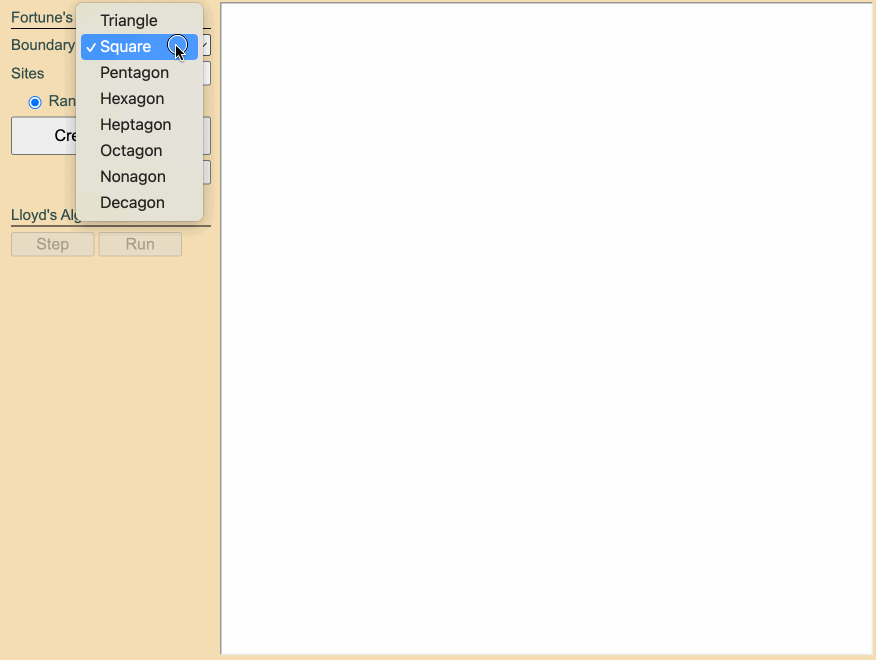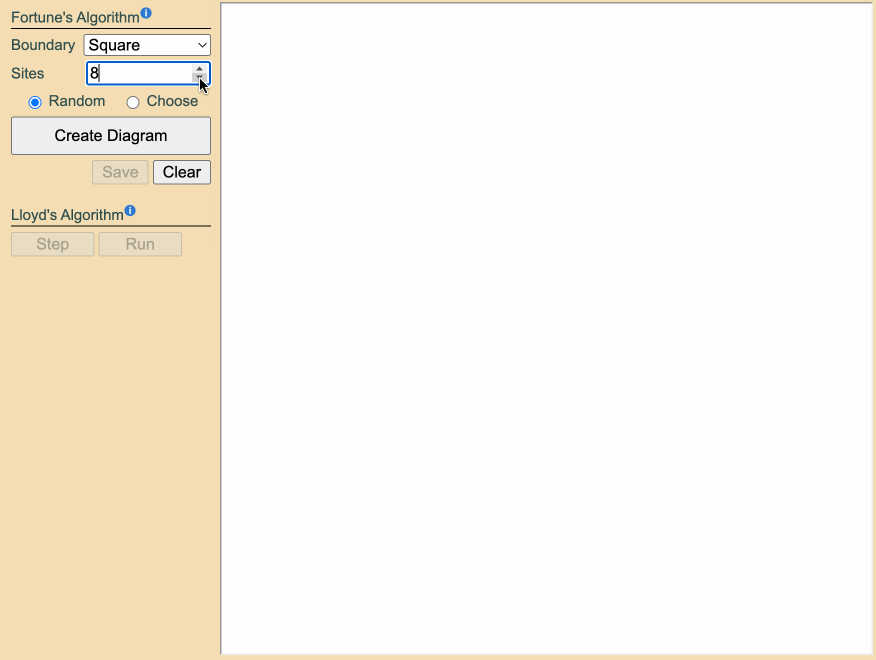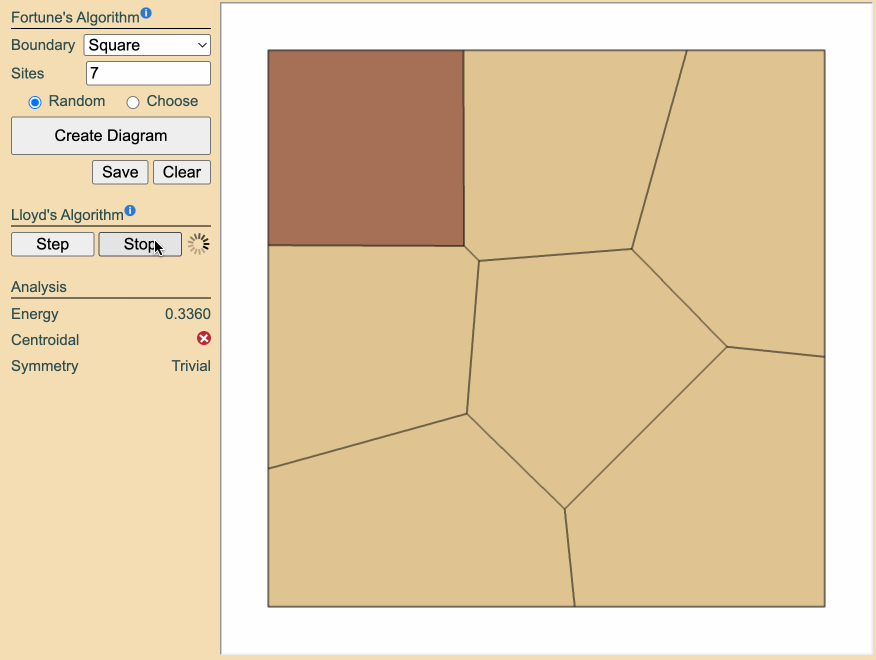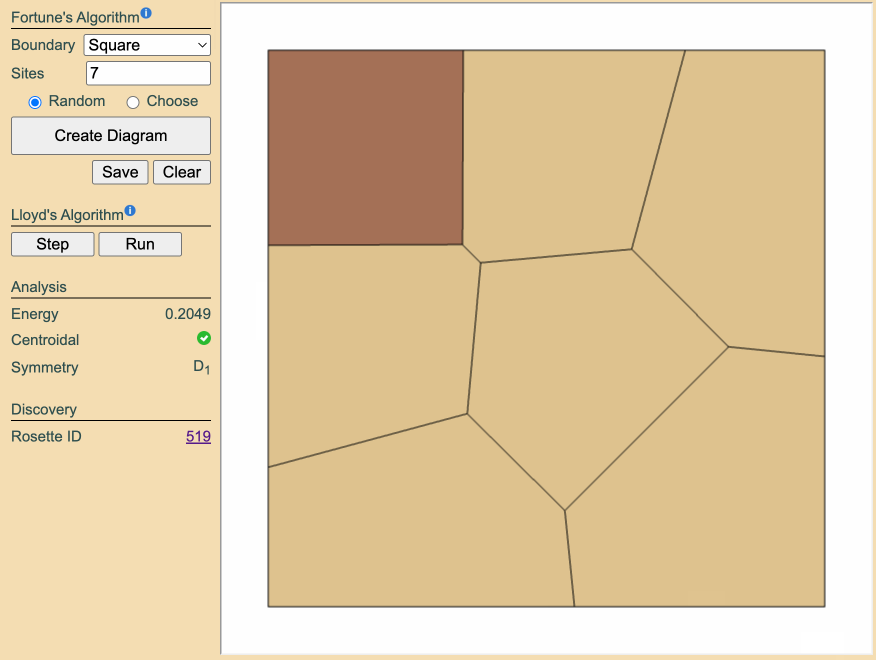
that, click Run to apply Lloyd's relaxation, transforming your diagram into a
centroidal Voronoi diagram-a Rosette.
Although quick and simple, this method relies heavily on randomness, providing only limited control over the resulting structure. Most Rosettes generated this way will either be trivial or have been previously discovered. To more deliberately create new Rosettes, we'll need to apply a bit of number theory to their symmetry models.
In mathematics, modular arithmetic is a system of operations on integers where numbers wrap around when reaching a certain value called the modulus. A familiar example is the 12-hour clock; 13 o'clock is read as (\(13 \bmod 12 = 1\)) 1 o'clock . We can use the same idea to uncover an invariant of rosettes that links the number of sites \(N\) to the rotation order \(r\) of its symmetry group.
Consider the cyclic rotation subgroup of order \(r\). When it acts on the set of \(N\) sites:
where \(f\) is the number of fixed (central) sites and \(m\) the number of full-size orbits. Reducing both sides modulo \(r\) gives
Hence the total site count \(N\) can leave only a remainder of 0 (no central site) or 1 (exactly one central site) when divided by \(r\).
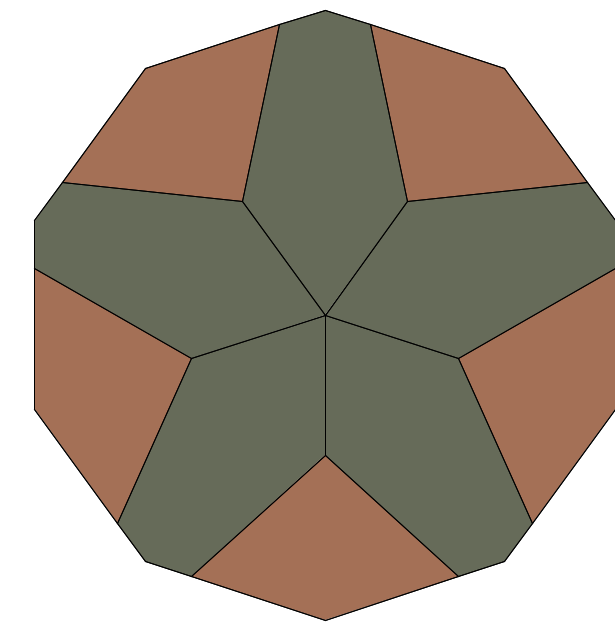A \(D_{5}\) decarose with \(N = 10\) sites, \(f = 0\) central sites.
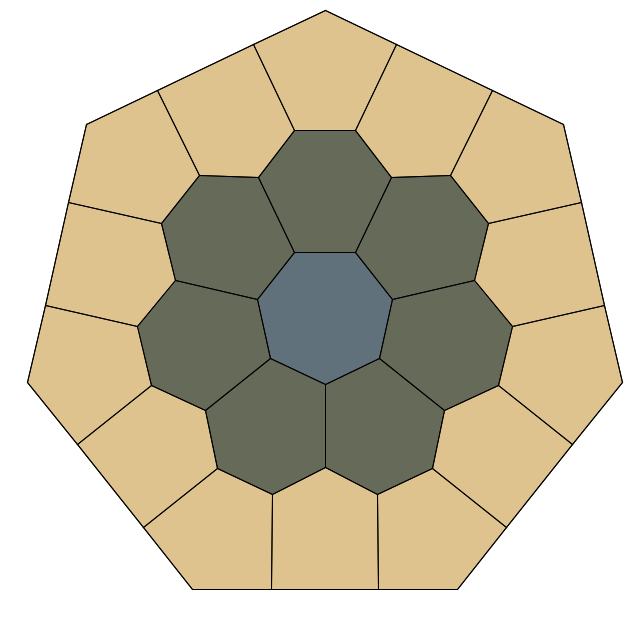A \(D_{7}\) heptarose with \(N = 22\) sites, \(f = 1\) central site.
Armed with this simple rule - \(N \bmod r = f \in \{0,1\}\) - rosette creation can be guided toward a specific symmetry order. Each valid value of \(N\) sends Lloyd's algorithm into a different region of the energy landscape, significantly improving the chance of finding a truly novel rosette.
Sometimes, symmetry alone isn't enough to guarantee a new or interesting Rosette. Even when the site count satisfies the modular condition, the random starting configuration will often land in a basin that funnels the diagram toward a trivial or common result. This is where shaping by hand comes in. Manually dragging sites (and their associated cells) before running Lloyd's relaxation subtly shifts the topology of the diagram-potentially unlocking access to entirely different local minima in the energy landscape. These small adjustments can dramatically alter the final result, especially when performed near the center or along key symmetry axes.
Sometimes the shortcut to a truly novel rosette lies not in adding or tweaking sites, but in removing them. Deleting an entire orbit of sites-a full set related by the diagram's symmetry-collapses the configuration into a new shape. Rerunning Lloyd's relaxation can then cause the system to slide into different local minima in the energy landscape that are otherwise unreachable.
What makes orbit deletion so powerful is that the "valleys" crossed in the energy landscape are themselves symmetric. Erasing an entire symmetry orbit enables traversal of those balanced pathways, unlocking minima that respect rotation but lie beyond the reach of random seeding or manual site manipulation.
